Deformable Convolutional Networks
Deformable Convolution
Standard convolution has fixed sampling location and receptive field. To solve this problem, Deformable convolution use learnable offset.
2D Convolution
The standard 2D convolution consists of two steps: 1) sampling using a regular grid \(\mathcal{R}\) over the input feature map \(\mathbf{x}\); 2) summation of sampled values weighted by \(\mathbf{w}\).
The receptive field size and dilation define the grid \(\mathcal{R}\). For example, when 3 X 3 kernel with dilation 1 the grid is:
\[\mathcal{R}=\{(-1, -1), (-1, 0), \ldots, (0,1), (1, 1)\}\]For each location \(\mathbf{p}_0\) on the output feature map \(\mathbf{y}\), 2D convolution can be denoted as followings:
\[\mathbf{y}(\mathbf{p}_0)=\sum_{\mathbf{p}_n\in\mathcal{R}}\mathbf{w}(\mathbf{p}_n)\cdot \mathbf{x}(\mathbf{p}_0+\mathbf{p}_n),\]2D Deformable Convolution
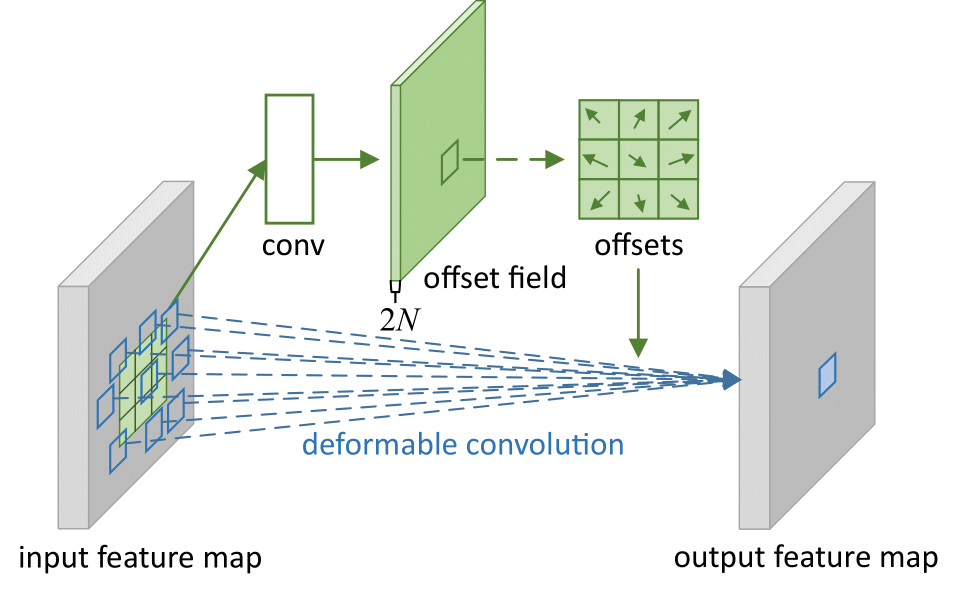
In deformable convolution, the regular grid \(\mathcal{R}\) is augmented with offsets \(\{\Delta \mathbf{p}_n \lvert n=1,...,N\}\), where \(N= \lvert \mathcal{R} \lvert\). In other words, offsets can be different per grid offset. The offsets are obtained by applying a convolution layer over same input feature map, which means the offsets are learned.
\[\mathbf{y}(\mathbf{p}_0)=\sum_{\mathbf{p}_n\in\mathcal{R}}\mathbf{w}(\mathbf{p}_n)\cdot \mathbf{x}(\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n).\]Now, the sampling is on the irregular because the offset \(\Delta \mathbf{p}_n\) is typically fractional. So \(\mathbf{x}(\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n)\) is implemented via bilinear interpolation as
\[\mathbf{x}(\mathbf{p})=\sum_\mathbf{q} G(\mathbf{q},\mathbf{p})\cdot \mathbf{x}(\mathbf{q}),\]where \(\mathbf{p}=\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n\) and \(\mathbf{q}\) is integral positions within 2 X 2 square which is centered with \(\mathbf{p}\). \(G(\cdot,\cdot)\) is the bilinear interpolation kernel and can be denoted as follows:
\[G(\mathbf{q},\mathbf{p})=(1- \lvert q_x-p_x \lvert ) \cdot (1- \lvert q_y-p_y \lvert )\]Result
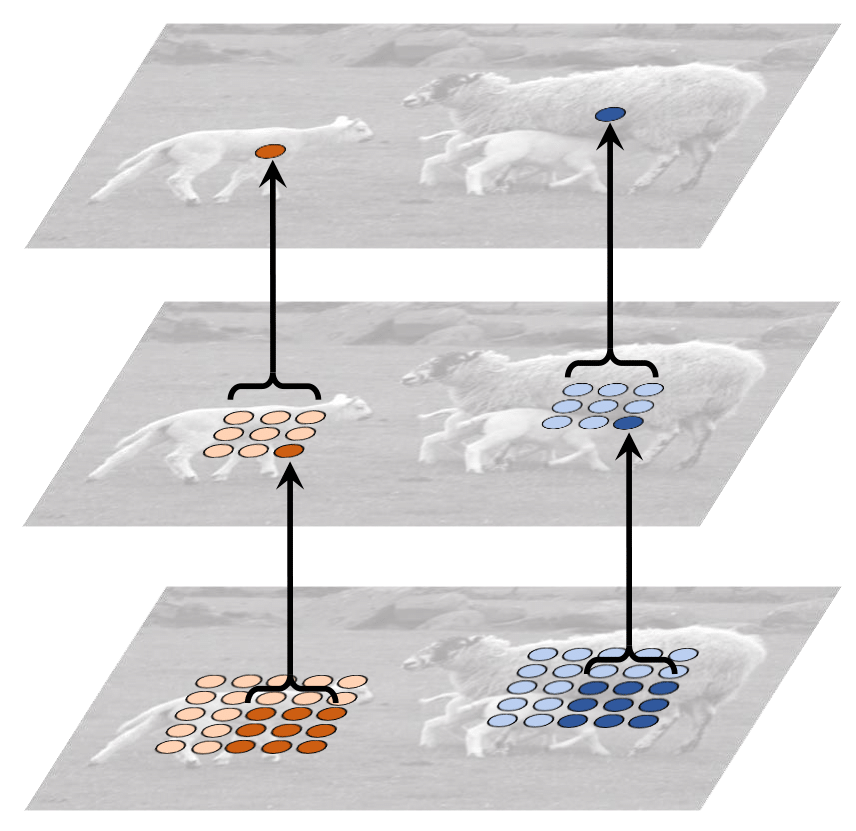
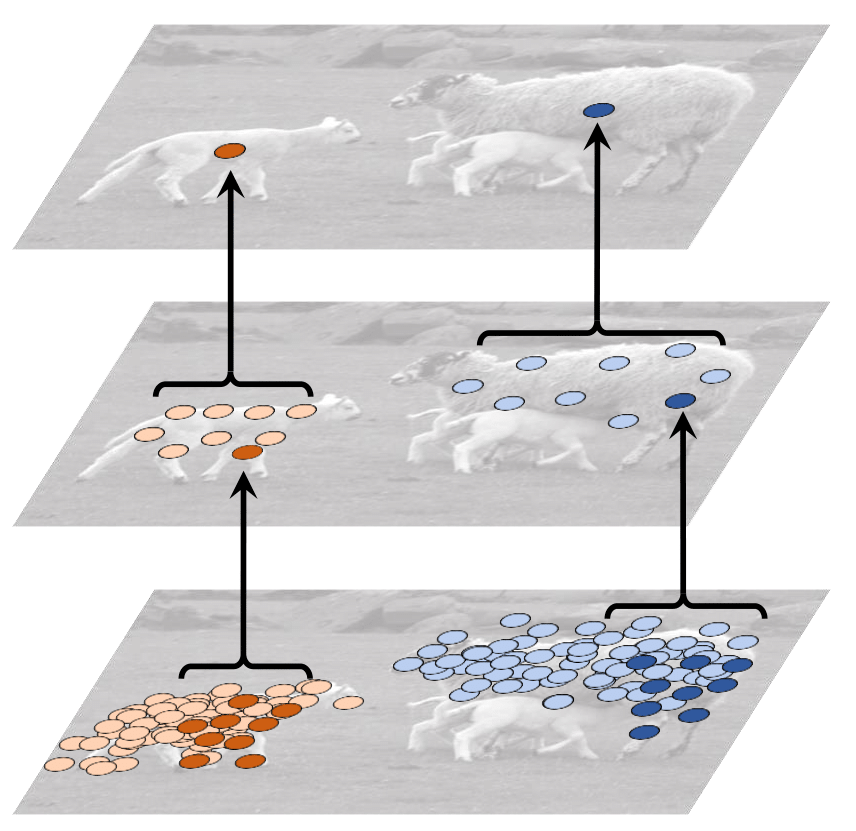
As Deformable convolution has offset on its grid, It can have more flexible receptive field.
| Standard Convolution | Deformable Convolution |
|---|---|
 |
 |